Making sense of Laziness

Aside:

These are my thoughts on lazy evaluation in programming languages, developed in the process of understanding laziness. I have written all of this down to make my life easier later on, and references exist to help me understand it. This isn’t supppose to be the definitve guide consider going through references and building your own understanding.

Laziness in terms of program evaluation strategy refers to the behavior of the program depending on the order in which the parts of the program are executed.

The idea is that the program will not evaluate the expression until it is needed, which “can” lead to better performance. Evaluation here is control flow and data flow in programs and laziness can be useful in several ways, such as eliminating dead code, auto pipelining or parallelizing code, etc.

The reason understanding these control flow semantics is important is because it helps us understand how our program will behave, and how we can improve it. For example, we can build simplified expressions that are easier to evaluate from a complex chain of expressions, without requiring the entire expression to be computed at compile-time.

example of strict evaluation

Copy
int baz(int a) {
    return a + 1;
}
int bar(int b) {
    return b + 10;
}
int foo(int x, int y) {
    int a = baz(x);
    int b = bar(y);
    return a + b; // returns 30
}

The execution of the above program flows as follows:

1. baz(x) is evaluated and returns x + 1
2. bar(y) is evaluated and returns y + 10
3. The program returned x + 1 + y + 10.

Here assuming we don’t precompute the value of a + b at compile time. The issue here is with above code, reduction based optimizations can’t be used at runtime but only at compile time, in any strict language. For example, we can inline¹ the functions and variables and build the final expression x + 1 + y + 10. Which can be optimized by the compilers generally at compile time.

For example in lazily evaluated programs, even if we don’t pre-compute the value of a + b at compile time, we can still optimize the program. Such as converting the final return expression to, x + y + 11. This reduces 1 instruction that we may have to execute at runtime.

but are the performance gains enough?

Lazily computing has a cost too, and that is increased memory usage at runtime as we don’t just keep the returned value in memory but store the entire expression. This becomes an issue whenever we are dealing with very large expressions or complex data structures.

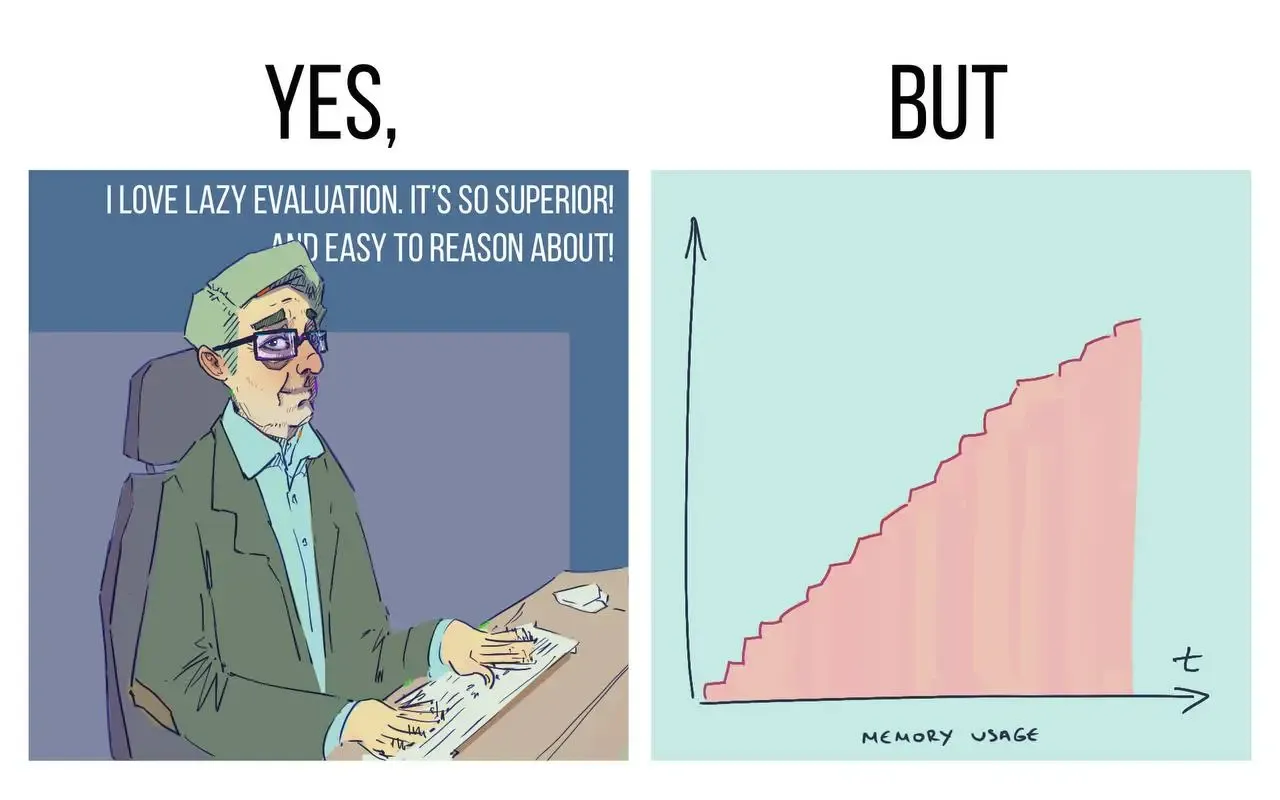
This means processing lots of data in a single pass is not efficient, with the cost of memory usage. In case of lazily computing, we can deal with such issues by making parts of the program strict so that we don’t have to store the entire expression.

For example, in Haskell the expression:

Copy
foldl (+) 0 [1..10^9]

Will consume memory for the entire list, because of laziness. That is above code will require atleast 400MB of memory, but the worst part is more memory used leads to greater loss of performance. This is cause the cost of fetching and accessing memory is much higher than compute for such code snippets in Haskell or any lazy programming language.

For this case you can use foldr instead of foldl:

Copy
foldr (+) 0 [1..10^9]

But in more complex cases where direction of operation evaluation is important, you can use foldl' or foldl. See foldr, foldl, foldl’.

but then, why laziness over strict evaluation

Haskell is the most popular programming language that supports laziness by default. The lazy evaluation in terms of Haskell is implemented in GHC compiler’s as non-strict² semantics.

That is, how a Haskell program computes expressions(it’s called non-strict semantics), which allows us to bypass undefined values(i.e. results of infinite loops) and consequentially work with formally infinite data structures.

understanding non-strictness in haskell

Haskell is one of the few modern languages to have non-strict semantics by default: nearly every other language has strict semantics, in which if any subexpression fails to have a value, the whole expression fails with it.

An example of this is the following program:

Copy
-- below function returns an infinte list
-- of the same value 'x'
repeat x = let xs = x : xs in xs

-- print 5, 15 times
main = print $ take 15 $ repeat 5

Haskell’s semantics for lazy evaluation is implemented in the form of thunks.³

brief intro to thunks

A thunk is a value that is yet to be evaluated. It is used in Haskell systems that implement non-strict semantics by lazy evaluation.

A lazy run-time system does not evaluate a thunk unless it has to. Expressions are translated into a graph and a Spineless Tagless G-machine⁴ reduces it, chucking out any unneeded thunk, unevaluated. An STG defines how the Haskell evaluation model should be efficiently implemented on standard hardware.

A thunk in practical terms is formed by every expression and sub-expression in Haskell, and since most things in the language are thunks(it’s a tad more complicated when considering GHC implementation but it’s a theoritically sound way of understanding it).

Copy
-- for example in the below
addOne :: Int -> Int
addOne x = x + 1
thunkedList :: [Int]
thunkedList = map addOne [0..100]

-- the list is thunked
-- we can force evaluate a part of it
-- by accessing its nth element
nthElem :: [Int] -> Int -> Int
nthElem list n = list !! (n - 1)

value :: Int
value = nthElem thunkedList 5

main :: IO ()
main = print value
-- will print 5
-- but the list will never be evaluated after 5th element

You maybe asking yourself about,

“How are thunks built?” Let’s take an recursive example to explain it.

Copy
-- recursion
repeat x = [x] ++ repeat x
-- = repeat 1
-- = [1] ++ repeat 1 // thunk
-- = [1] ++ [1] ++ repeat 1  // thunk
-- = [1] ++ [1] ++ [1] ++ repeat 1 // thunk
-- = [1] ++ [1] ++ [1] ++ [1] ++ repeat 1 // thunk
-- = [1] ++ [1] ++ [1] ++ [1] ++ [1] ++ repeat 1 // thunk
-- = [1] ++ [1] ++ [1] ++ [1] ++ [1] ++ [1] ++ repeat 1 // thunk
-- so on you get infinite thunks which you can compute and resolve when you need the value
-- let statements perform better for similar cases

Let statements are better for dealing with lazy code in general primarily due to expression sharing⁵. There is also the concept of let placement for optimizations by procuding better transformations, which should ideally be handled by a good optimizing compiler but reality can be harsh.⁶

”laziness keeps you pure”

As SPJ says, laziness keeps you pure, in his talk at Microsoft about Haskell.⁷

This may not mean we can’t have lazy evaluation in an impure language, but it is a lot more convenient to reason about lazy code when it’s assumed to be side-effect free, aka pure.

To explain further, imagine if you have a block of code to read from a database, process the query, ask user for input and then write to the database.

Now if you have a function that reads from the database, and another function that processes the query, and another function that writes to the database. It becomes important to run them in-order.

We can’t run them out of order or in parallel which both means we don’t make any gains from lazily evaluation and breaks our ability to reason about the laziness of the code. As each action may block the other in terms of synchronization, so they need to each be completed entirely before we can continue.

This promotes a need for maintaining clear boundaries between pure and lazy code and side-effectful impure code, a la, IO monad.

Aside

I have been considering documenting STGs notes as well feel free to follow the RSS for it. Note: I post about a lot of random things here, sorry if find them noisy I am considering setting up channels with modern atom rss and also supporting activitypub.